McCulloch Pitts Neuron

In 1943, McCulloch, a Neuroscientist and Pitts, a logician, proposed a simple computational model of the neuron discussed in the previous section.

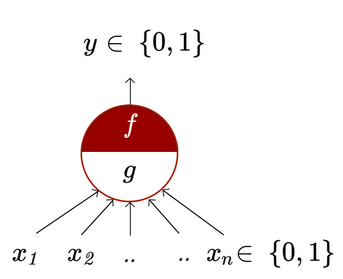
In this model, a series of Boolean inputs $x_1,x_2,...,x_n\in [0,1]$ are aggregated (i.e., summed up) by a function $g$ and another function $f$ takes a Boolean decision based on this aggregation. The output of $f$ is $y\in [0,1]$. Inputs can be excitatory or inhibitory. Inhibitory inputs are those that act as deal breakers, of sorts. If they are true, the output will be false, regardless of how the other inputs behave. Mathematically, this can be summarised as:

$$g(x_1,x_2,...,x_n)=g(x)=\sum _{i=1}^n{x}_i$$ $$y=f(g(x))=1ifg(x)\ge \theta$$ $$y=0ifg(x)<\theta$$

The threshold in question is $\theta$.

Let’s present the AND function using a McCulloch Pitts Neuron. If we take 2 inputs $x_1,x_2$, both of them must be 1 for the output to be 1 (true). Hence the threshold $\theta$ is 2.

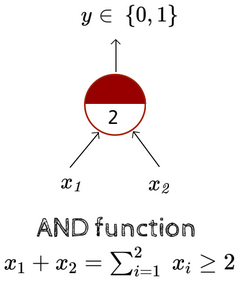
Of the four possible $(x_1,x_2)$ pairings, only one of them will output 1. Plotting the line $x_1+x_2=2$, we notice the following:

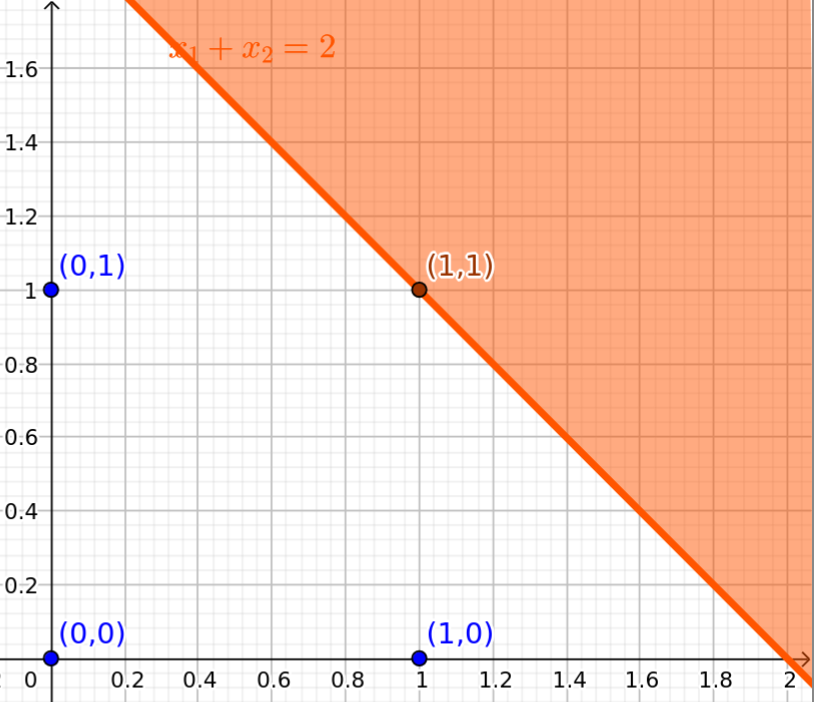
The line acts a linear separator - all input pairings such that $x_1+x_2\ge 2$, are on one side of the graph and will produce an output of 1. This is the positive half-space of the plot. All other points will produce an output of 0. The space occupied by these points are known as the negative half-space.

If we have more than 2 inputs, we will have a plane rather than a line. It must be noted that not boolean functions are linearly separable. The AND and OR function are, but the XOR function, for example, is not.