Introduction to Perceptrons

The McCulloch Pitts Neuron applies to boolean inputs with equal weightage and linearly separable functions. What about instances where the inputs are not Boolean (real numbers, for example) or some inputs are more important than others? Or what if we’re dealing with functions that are not linearly separable?

Perceptrons are a more broadly applicable version of the MP neurons that were conceived by Frank Rosenblatt, a Psychologist and refined and by Minsky and Papert.

Perceptrons allow weights to be assigned to the inputs and provide a mechanism to learn these weights. Inputs are also not limited to Boolean values.

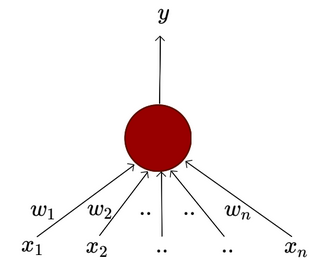
Including the weights for the different inputs, we get the following mathematical picture:

$$y=1if\sum _{i=1}^n{w}_i\ast x_i\ge \theta$$ $$y=0if\sum _{i=1}^n{w}_i\ast x_i<\theta$$

The conventional way of expressing the above inequalities is to have a dummy weight and input $w_0,x_0$ such that $w_0=-\theta$ and $x_0=1$. Rewriting the inequalities in this fashion, we get:

$$y=1if\sum _{i=0}^n{w}_i\ast x_i\ge 0$$ $$y=0if\sum _{i=0}^n{w}_i\ast x_i<0$$

The $-\theta$ is called the bias, since it represents a prior inclination or prejudice. It acts a threshold that needs to be offset by the sum of the products inputs and their weights. For example, if I am contemplating whether to watch a movie tonight, my bias would be rather low if I’m a movie buff. If not, it would take a lot of convincing, denoting a high bias.

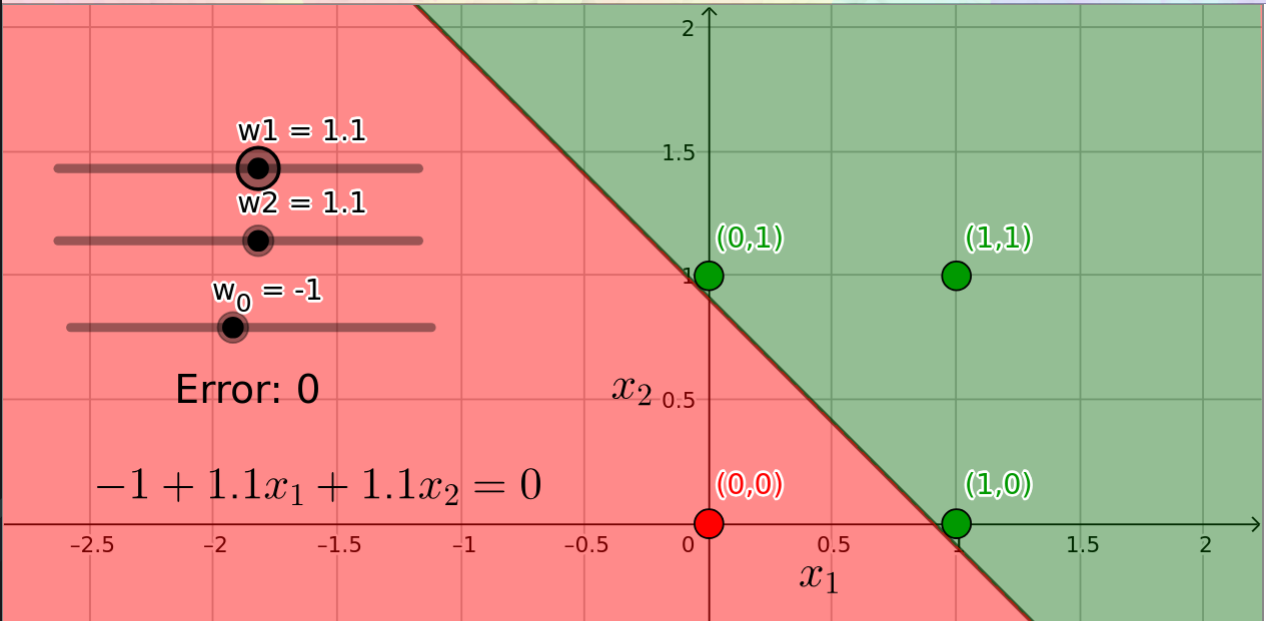
Like MP Neurons, Perceptrons also separate the input space into two halves. Therefore, they too, can only be used to plot linearly separable functions. If we analyze the OR function with 2 inputs, there are four possible input pairings - $(1,1),(1,0),(0,1),(0,0)$. Three of these will return true. If $w_1,w_2$ are the weights assigned to the two features with $w_0$ being the bias, we get the following set of inequalities:

$$w_0+w_1\ast 1+w_2\ast 1\ge 0⟹w_0\ge -w_1-w_2$$ $$w_0+w_1\ast 1+w_2\ast 0\ge 0⟹w_0\ge -w_1$$ $$w_0+w_1\ast 0+w_2\ast 1\ge 0⟹w_0\ge -w_2$$ $$w_0+w_1\ast 0+w_2\ast 0<0⟹w_0<-w_1-w_2$$

All valid solutions must satisfy these constraints to be included in the input space for the OR function. Among others, one possible solution to this set is $w_0=-1,w_1=1.1,w_2=1.1$.