Perceptron Learning Algorithm

The Perceptron Learning Algorithm (PLA) is a principled way of learning the weights assigned to the input points such that the error between the prediction made the Perceptron model and the actual label of the inputs is minimal. Convergence is said to have occurred when all the points are classified correctly. The following screenshot explains the algorithm in pseudocode:

$x$ is the input vector $[x_0,x_1,...,x_n]$ and $w$ is the weight vector $[w_0,w_1,...,w_n]$. The algorithm says that if we have a positive point, which is incorrectly classified as negative, we must add that point to the weight vector. Similarly, negative points wrongly classified as positive must be subtracted from the weight vector. The perceptron algorithm states that:

$$y=1if\sum _{i=1}^n{w}_i\ast x_i\ge \theta$$ $$y=0if\sum _{i=1}^n{w}_i\ast x_i<\theta$$

${\sum }_{i=1}^n{w}_i\ast x_i$ is basically the dot product of the weight vector and input vector: $w^{T}x$. Hence we are interested in finding the plane $w^{T}x=0$ which neatly divides the input space into two halves. All points that lie on this line are perpendicular to the weight vector since $cos\alpha =\frac{w^{T}x}{||w||||x||}=0⟹\alpha =90$.

Points that lie on the positive half-space of the input space (i.e., $w^{T}x>0$) form an angle less than $90°$ with the weight vector while those in the negative half-space form an angle less than $90°$. The following figure demonstrates this:

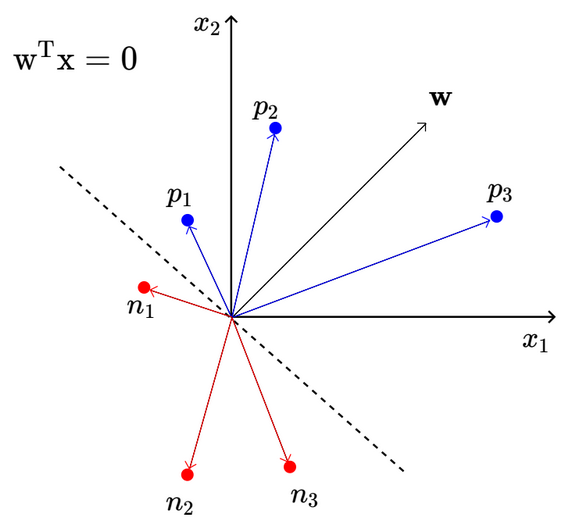
$p_1,p_2,p_3$ represent the points in the positive half-space while $n_1,n_2,n_3$ are the points in the negative half-space. This means that positive points that are misclassified form an angle greater than $90°$ with the current weight vector, but we want it to be less. As per the algorithm, if a positive point $x$ is misclassified, we add it to the weight vector, forming $w_{new}=w+x$. Therefore:

$$cos({\alpha }_{new})\propto (w_{new}{)}^{T}x$$ $$cos({\alpha }_{new})\propto (w+x{)}^{T}x$$ $$cos({\alpha }_{new})\propto w^{T}x+x^{T}x$$ $$cos({\alpha }_{new})\propto cos(\alpha )+x^{T}x$$ $$cos({\alpha }_{new})>cos\alpha$$

Hence, ${\alpha }_{new}<\alpha$. This shows that upon adding the point to the weight vector, the angle it forms with the weight vector, now updated, is less than what it was. It may not be possible to bring the angle below $90°$ in one shot but inches us closer to that goal. Naturally, the same logic would apply if a negative point is misclassified, meaning that the angle it forms with the weight vector is less than what we’d like it to be. We subtract such a point from the weight vector.

This shows us that updating the weight vector according to the above method could make the algorithm converge. However, since we’re picking input values at random and updating the weight vector based on their state, how do we know that the algorithm won’t keep flip-flopping between different values infinitely? For example, one input element could add to the weight vector but the next could subtract from it and bring it back to the previous value and this could go on forever.