Proof of Convergence

If we have two sets $P$ and $N$ such that the former contains all the positive points in the input space and the latter contains all the negative points, how can we prove that the PLA will converge for a linearly separable dataset? In other words, how can we address the concern from the previous section, that the updating of the weight vector could go on forever, without cleanly separating the positive points from the negative points at the end? For the PLA to be valid the number of times the weights are updated needs to be finite.

Let’s consider a new set $P^{\prime }=P\cup N^{-}$. In the RHS, $N^{-}$ is the negation of $N$, meaning that we flip the signs of all those points for which ${\sum }_{i=1}^n{w}_i\ast x_i<w_0$. Every $p\in P^{\prime }$ will satisfy $w^{T}p\ge 0$. Further we normalise all the p’s such that $||p|{|}^2=1$. $w^{\ast }$ will the solution weight vector for this normalised set.

With that established, the following screenshot has the pseudocode for this slightly modified PLA:

Notice that we have only one if loop this time since all points in $P^{\prime }$ are positive. $w^{\ast }$ is the optimal solution, but we don’t know what it is yet. It gets updated each time $w^T{p}_i\le 0$. It need not be updated after every iteration. Hence, after $t$ iterations, the total number of updates $k$ will be less than $t$. Now, let’s say at the $t^{th}$ iteration, we see a misclassification for point $p_i$. We correct that giving us $w_{t+1}=w_t+p_i$. If $\beta$ is the angle between $w^{\ast }$ and $w_{t+1}$:

$$cos\beta =\frac{w^{\ast }{w}_{t+1}}{||w_{t+1}||}$$

Upon performing some computations on the numerator and denominator of the above, we get:

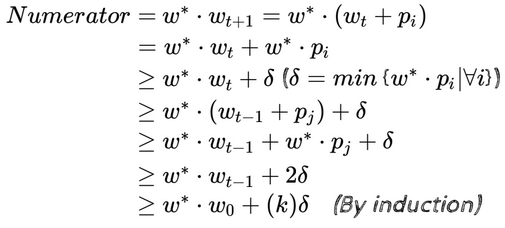
Combining the 2 results, we get:

$$cos\beta \ge \frac{w^{\ast }{w}_0+k\delta }{\sqrt{||w_0|{|}^2+k}}$$

This means that $cos\beta$ grows proportionally to $\sqrt{k}$. As $k$ increases, $cos\beta$ could become arbitrarily large. However, $cos\beta$ has to be $\le 1$, which means that $k$ will be bounded too. This proves that the number of updates made to the weight vector will be a finite and the PLA will converge at some point.