Linearly Inseparable Functions

Till now, we have focused entirely on linearly separable functions since single Perceptrons cannot implement functions that aren’t separable. Most functions in the real world aren’t linearly separable and we therefore need a model to deal with them. A network of Perceptrons, as opposed to a single one, could do the trick. One such inseparable function is the XOR function.

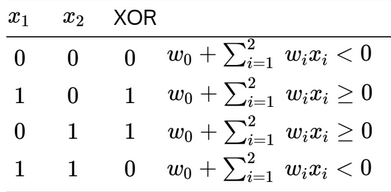
From the table, we derive the following set of inequalities:

$$w_0+w_1\ast 0+w_2\ast 0<0⟹w_0<0$$ $$w_0+w_1\ast 0+w_2\ast 1\ge 0⟹w_2\ge -w_0$$ $$w_0+w_1\ast 1+w_2\ast 0\ge 0⟹w_1\ge -w_0$$ $$w_0+w_1\ast 1+w_1\ast 1<0⟹w_1+w_2<-w_0$$

• The fourth inequality contradicts the second and third, meaning that isn’t a linearly separable function.

If we have 2 inputs, how many Boolean functions can we create with them? Since there are 4 possible inputs - $(0,0),(0,1),(1,0),(1,1)$ there are possible 16 combinations of outputs. This generalises to $2^{2^n}$ for $n$ inputs. Of these functions, the number of them that are linearly separable is hard to tell.

Getting back to dealing with linearly inseparable functions, let’s assume $n=2$ and a network of Perceptrons, each of which is connected to both the inputs with specific weights, either 1 or -1, which are hard-coded. The bias $w_0$ is assumed to be $-2$ and the output $y$ of this network is either $1$ or $-1$. The output of each perceptron in the network is $h_1,h_2,...,h_n$ and these outputs are assigned weights $w_1,w_2...,w_n$ which need to be learned.

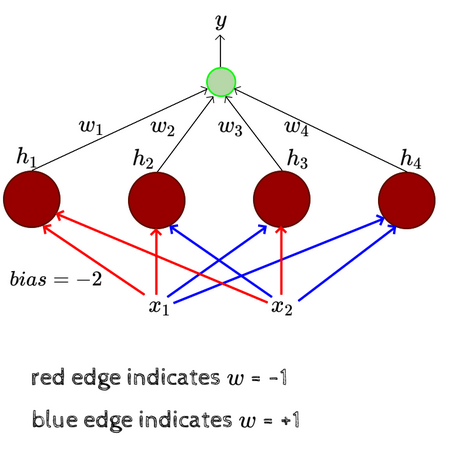This network contains 3 layers:

• The layer that contains the inputs is the input layer.
• The layer with the 4 perceptrons is the hidden layer.
• The layer containing the output neuron is the output layer.

$h_1$ to $h_4$ are the outputs of the perceptrons in the hidden layer. The red and blue edges are called layer 1 weights while $w_1$ to $w_4$ are called layer 2 weights. Note that the layer 1 weights are hard-coded and assigned purposefully. The layer 2 weights, on the other hand, need to be learned. This network can be used to learn any Boolean function, regardless of whether it’s linearly separable.

If we take a close look at how the layer 1 weights are assigned, we see that each perceptron in the hidden layer fires only for a particular input. Let’s take the input $(-1,-1)$. The weighted sum of the first perceptron will be $-2+(-1\ast -1)+(-1\ast -1)$ which is greater than $0$ and will hence fire. For the second perceptron the weighted sum will be $-2+(-1\ast -1)+(-1\ast 1)$ which is less than $0$ and will not fire. Looking at each of the four possible inputs and computing the weighted sum for each perceptron, we notice that only one of the perceptrons in the hidden layer will fire, as long as we engineer the layer 1 weights in a particular manner.

If $w_0$ is the bias assigned to the hidden layer, the output $y$ will be $1$ if ${\sum }_{i=1}^n{w}_i{h}_i\ge w_0$ else $0$. In the above example, the input $(-1,-1$) meant that only the first perceptron in the hidden layer fired, meaning that ${\sum }_{i=1}^4{w}_i{h}_i=w_1$ since $h_1=1$. All the other h’s are 0. For other inputs, each of the other 3 perceptrons would fire and the weighted sum will be the respective weight. Now, if we look at the XOR function with such a network, it can be implemented:

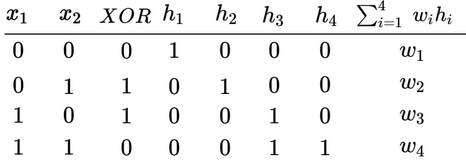
• 0 should be replaced by -1.

Each $w_i$ is responsible for one of the four possible inputs. If we write out the set of inequalities, there won’t be any contradictions, meaning that the function can be implemented.

Such a network can be used to implement all the other possible boolean function as well and can be used for any number of inputs. However, the catch is that as $n$ starts to grow, the number of perceptrons in the hidden layer increases exponentially.