Till now, we’ve dealt only with Boolean functions. How can we deal with real functions where , instead of ?
Recall that a perceptron fires (i.e., returns 1) if the sum of its weighted inputs is greater than a threshold . Looking at the example of whether we will watch a movie or not, let’s say there’s only one input, which the movie’s average rating given by critics. If the threshold is 0.5 and , we would conclude that we would indeed watch the movie if the average rating was but wouldn’t watch it if the rating was , since they fall on either side of the threshold. This seems harsh, since our decision sways completely to other side when we cross the threshold. A rating of is the same as in this context. This is a characteristic of the perceptron function, which is a step function.
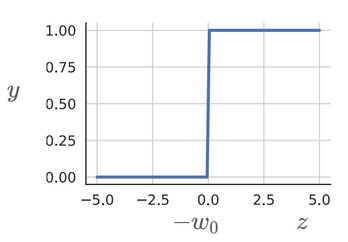
A function which would shift gradually from 0 to 1 would be better than one which takes only either extreme. The sigmoid function is one such example. It is expressed as:
We don’t see a sharp shift from one side to another when we cross the threshold.
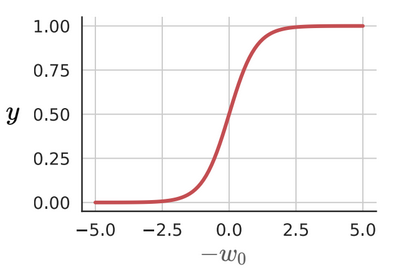
The output y here is not binary, but is a real value between 0 and 1. Naturally, this can be interpreted as a probability too. Further, the sigmoid function is continuous and differentiable.