Approximating Functions Using Taylor Series

The Taylor Series is a way of approximating continuously differentiable functions within a particular window using polynomials of degree $n$. The higher the degree, the better the approximation. For example, if we have the function $ln(x)$, its linear approximation ($n=1$) would look like this:

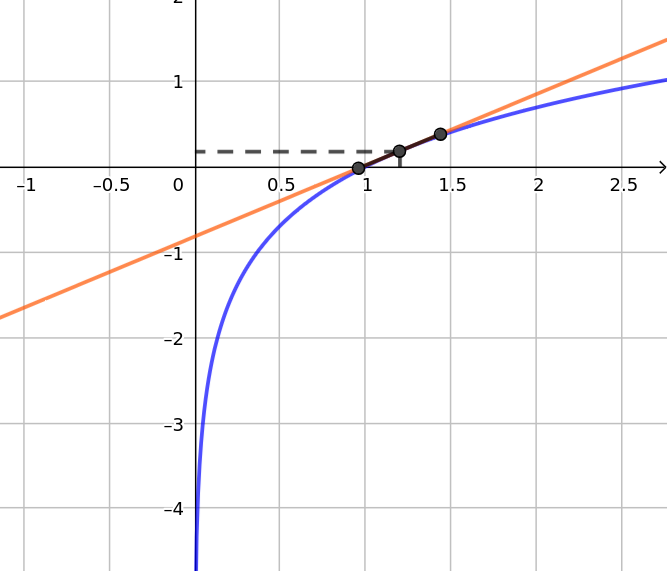
Notice that outside the interval marked by the black points, linear approximation does not provide an accurate picture of the original function.Hence, we’d like as small an interval as possible. A quadratic approximation of $ln(x)$ would look like:

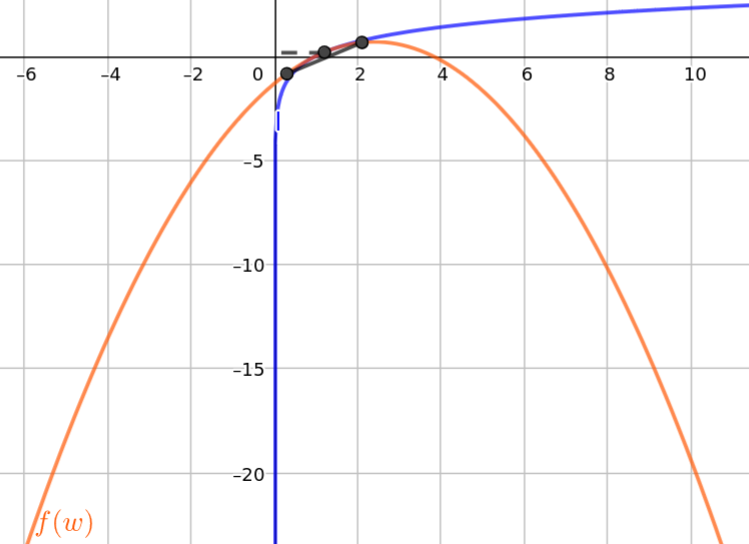
This is a more accurate approximation than the linear one.

If we know the value of a function at a particular point, we can approximate the value at a different point near it based on our chosen degree of approximation. If we’d like to approximate our loss function and we know the value of the function at $w_0$, we can approximate the function’s value at a point $w$ as follows:

• Linear approximation:

$$\ell (w)=\ell (w_0)+\frac{{\ell }^{\prime }(w_0)}{1!}(w-w_0)$$

• Quadratic:

$$\ell (w)=\ell (w_0)+\frac{{\ell }^{\prime }(w_0)}{1!}(w-w_0)+\frac{{\ell }^{\prime \prime }(w_0)}{2!}(w-w_0{)}^2$$

${\ell }^{\prime }$ and ${\ell }^{\prime \prime }$ refer to the first and second order derivatives of the function.