We have seen that a multilayered network of Perceptrons, with one hidden layer, can be used to represent any boolean function precisely. Represent, in this context, means that we could pass an input to the network of perceptrons, and it would give us the correct output based on the truth table for that function.
Similarly, a multilayered network of sigmoid neurons can be used to approximately represent any continuous function to any degree of precision. If is the output of our approximation and is the real output, for each input, where is the degree of precision desired. This is known as the Universal Approximation Theorem (UAT).
Any function we’re trying to represent can be shown as a collection of towers under the curve. For example:
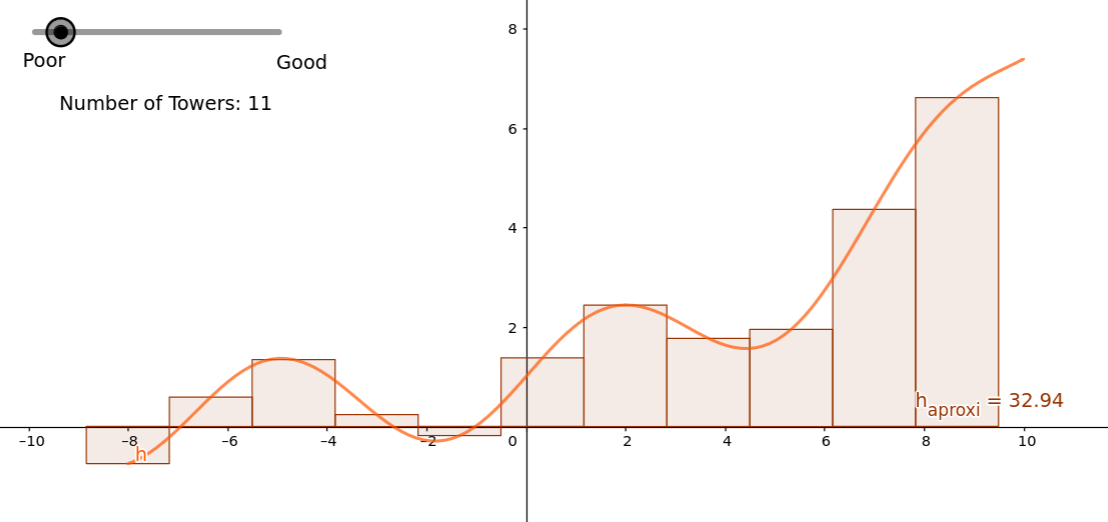
Naturally, if we increased the number of towers, we could get a more precise representation of the underlying function.
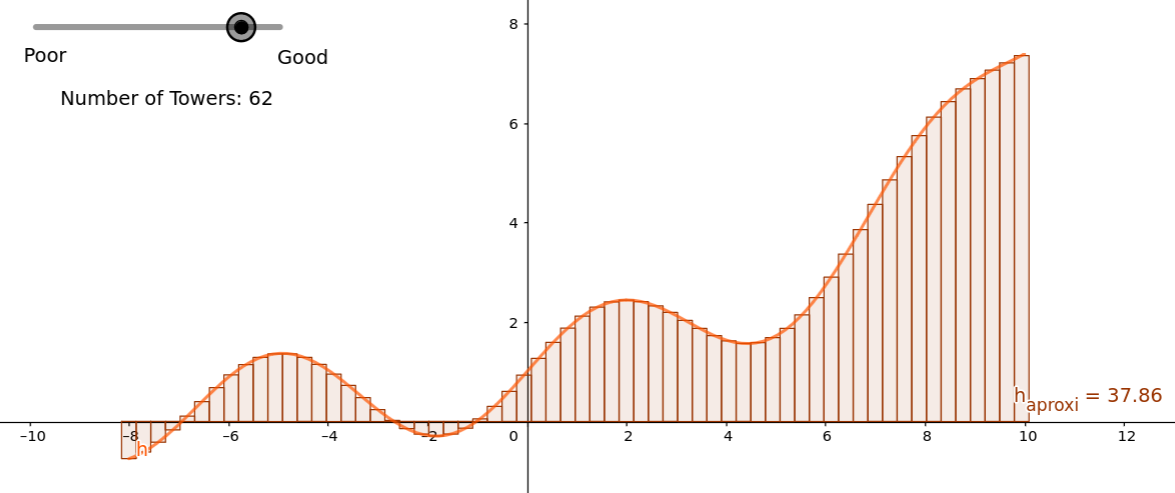
We can think of this as an environment where there’s a black-box function that takes an input and created a bunch of towers, of varying heights and puts them all together, forming an approximation of some function.
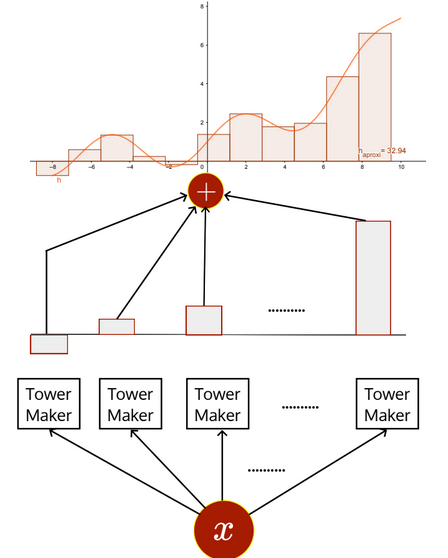
What is this black-box that creates these towers and aggregates them?
Going back to neural networks and sigmoid neurons, let’s say we have a network with one input and one hidden layer with two neurons in it. Let the weight and bias of the two neurons in the hidden layer be and respectively. For any sigmoid function, if we set to be high enough, it effectively becomes a step function since increasing makes the curve steeper. , on the other hand, is a horizontal line.
Let’s set and very high, meaning that for both neurons in hidden layer, the activation functions in the hidden layer are step functions. With these two step functions in place, what if we subtracted one from the other? We essentially get a tower function:
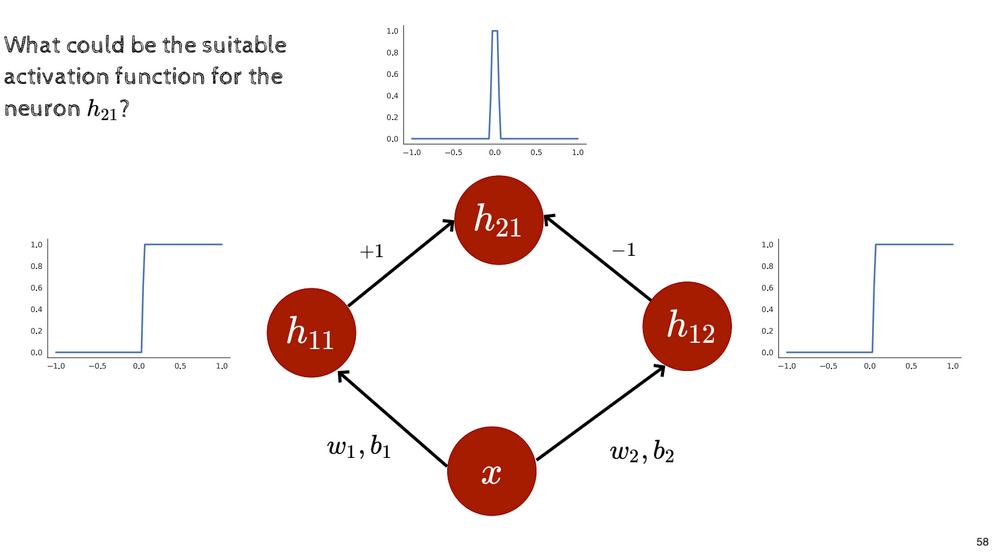
Representing the weights of and are and is the same as subtracting the second from the first. These two neurons come together and form a new neuron , which represents a tower function. This proves that with a multilayered network of sigmoid neurons, we can generate tower functions, which can in turn be used to represent any function, such as the sigmoid.
This example explains how tower functions can be created when there’s only input. What if there are 2 inputs? How can 2D tower functions be generated?
The procedure is largely the same, except that the number of neurons required would increase since there’s an extra dimension and two extra sides that need to be dealt with. The following image displays a 2D tower function:
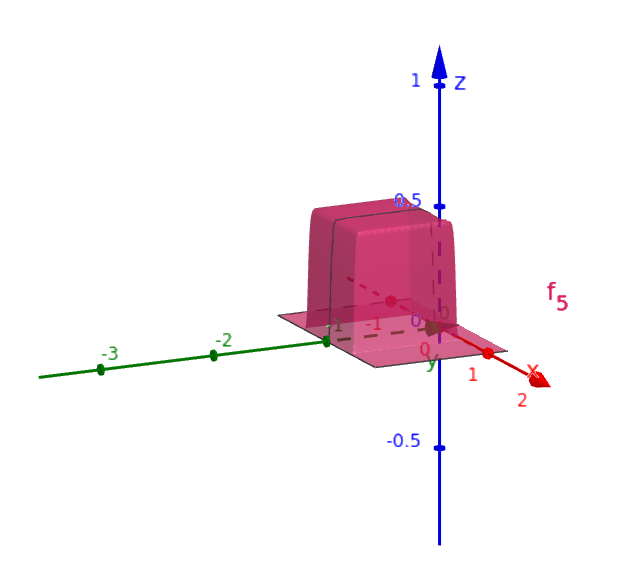
The requirement for an increased number of neurons is displayed by this diagram:
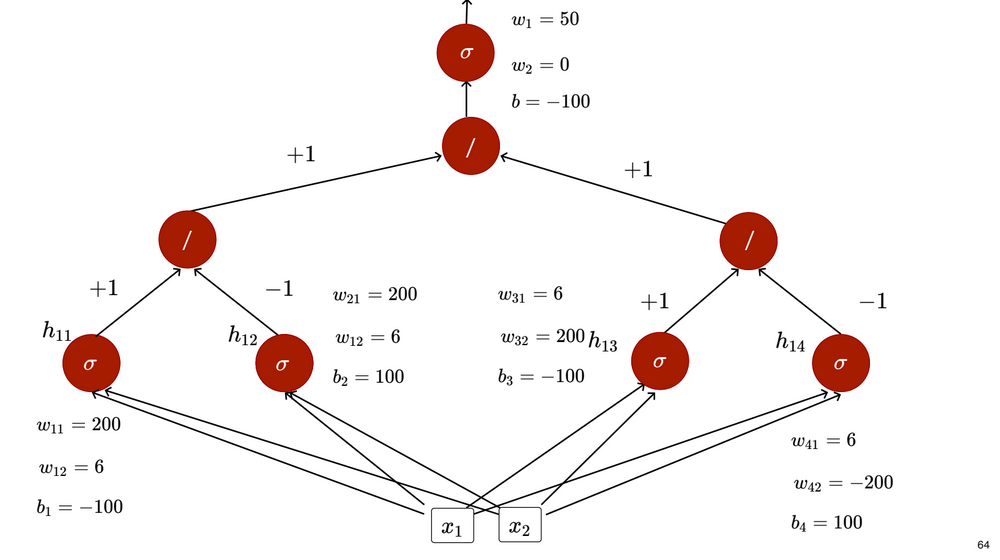
With one input, we needed 2 neurons in the hidden layer and with 2 inputs, we needed 4 hidden layer neurons. This means that the number of neurons required in the hidden layer is twice the number of inputs.