Feed Forward Neural Networks

Feedforward neural networks are defined by DeepAI as:

A feedforward neural network is one of the simplest types of artificial neural networks devised. In this network, the information moves in only one direction—forward—from the input nodes, through the hidden nodes (if any), and to the output nodes.

The input to such a network is an $n$-dimensional vector. The network contains $L$ layers with $L-1$ hidden layers and one output layer. The input layer is considered to be the $0^{th}$ layer. Let’s assume that each hidden layer consists of $n$ neurons and the output layer has $k$ neurons.

Each neurons in the hidden layers and the output layer consists of a pre-activation part $a_i$ and an activation part $h_i$. Each input $x_i$ has a weight to every neuron in the first hidden. Similarly, every neuron in each hidden layer has a weight to each neuron in the layer coming after it. Each neuron in each layer has a bias attached to it too. This setup is represented by the following diagram:

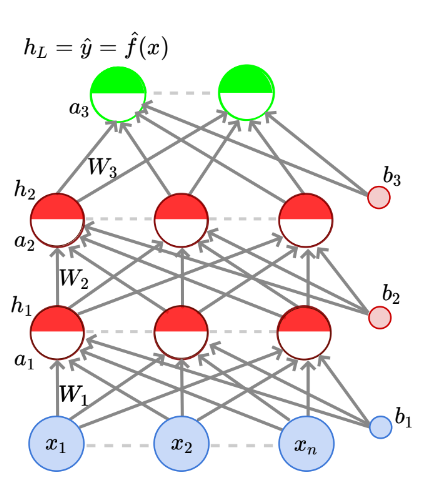
Putting all the input variables together, we get the input vector $x\in R^n$. Each neuron of a hidden layer has $n$ weights (for each neuron/input from the previous layer). If combine the weight vectors for all the neurons in a particular layer, we get an $n\times n$ matrix. Hence, $W_i\in R^{n\times n}$. Similarly, since each neuron in a layer has a bias, the bias vector for the entire layer is in $R^n$ i.e., $b_i\in R^n$.

The pre-activation part of each neuron takes the weighted sum of the outputs from the previous layer and adds the bias to it. Remember that all these computations are done with vectors since bring all inputs, weights and biases into its respective vectors. The calculation of the activation for the first hidden layer, assuming $n=3$ would be:

$$a_1=\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ a_{13}\end{array}\right]=\left[\begin{array}{c}{b}_{11}\\ b_{12}\\ b_{13}\end{array}\right]+\left[\begin{array}{ccc}{w}_{111}& w_{112}& w_{113}\\ w_{121}& w_{122}& w_{123}\\ w_{131}& w_{132}& w_{133}\end{array}\right]\ast \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$

• For the second hidden layer onwards, $x$ should be replaced by $h$.

Writing the above in a generic form, we get:

$$a_i=b_i+W_i\ast h_{i-1}$$

The activation part of the neuron takes the pre-activation part’s output and applies a function on it. This function could logistic, tanh, linear, among others.

$$h_i=g(a_i)$$

• $g$ is called the activation function.

The activation in the output layer, which uses different notation is:

$$f(x)=h_L=O(a_L)$$

Using the manner in which supervised learning setups are typically represented, we can represent this situation in the following manner:

Data: ${x_i,y_i}_{i=1}^N$

Model: $\hat{y}=\hat{f}(x_i)=O(W_{3g}(W_{2g}(W_{1}x+b_1)+b_2+b_3$

• This is just how the compuation would look like if we wrote out the calculations for each hidden layer together.

Parameters: $\theta =W_1,...,W_L,b_1,b_2,...,b_L$

Algorithm: Gradient Descent with backpropagation (covered soon)

Loss function: $\mathcal{L}(\theta )=min\frac{1}{N}{\sum }_{i=1}^N{\sum }_{j=1}^k({\hat{y}}_{ij}-y_{ij}{)}^2$

• This takes the squared sum of the difference between the predicted output and the real output and then average the squared error for all points in the training data.