Feed Forward Neural Networks: Output and Loss Functions

The choice of output and loss functions for a feedforward neural network depends on the nature of the problem at hand.

Let’s say we have a Regression problem, which seeks to predict the IMDB and Letterboxd rating for a movie, with 2 inputs variables - whether the movie has a good plot and if its dialogues are good:

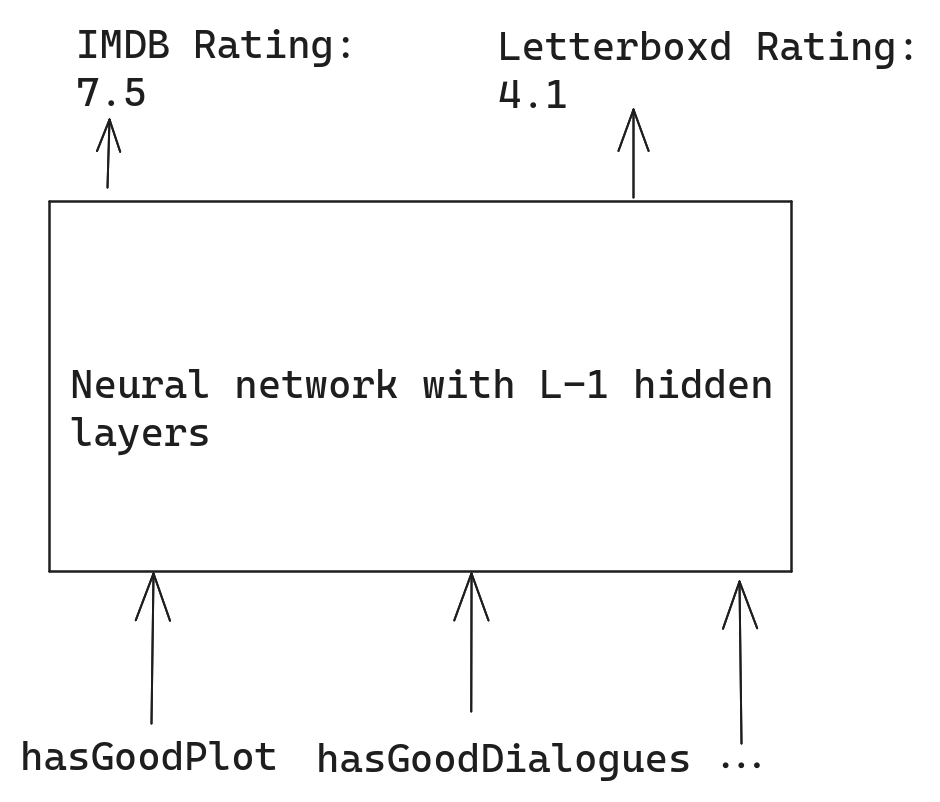
This means that $x\in R^2$ and $y\in R^2$. The loss function should capture how much our prediction $\hat{y}$ differs from the actual output $y$. In this case, the squared error would work:

$$\mathcal{L}(\theta )=\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^k({\hat{y}}_{ij}-y_{ij}{)}^2$$

But before that, what should the output function be? In other words, what function should be applied to the pre-activation part of the output layer of the network. In this case, since we don’t the output to be bound between 0 and 1, a linear function would be better than the sigmoid function.

What about Classification problems?

Let’s say we have an image of a fruit and we’d like to predict whether it’s a Mango, Orange, Apple or Banana. Here, $y\in R^4$ but among the 4 positions in the vector, only one of them will be 1 and the rest will be 0 since the image can only represent one fruit.

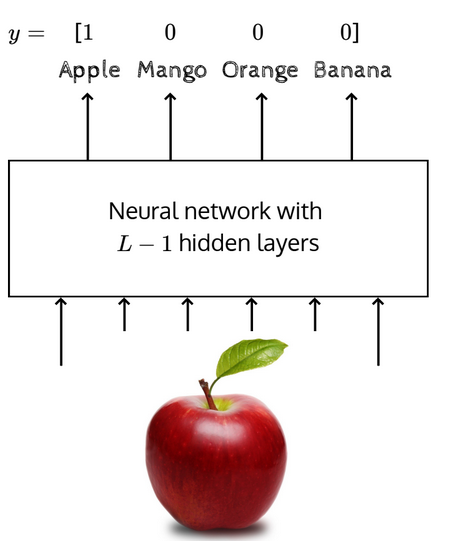
In classification tasks, we try to predict the probability of the various possible outputs. Hence, the output function should be one that ensure that our prediction vector $\hat{y}$ is a probability distribution. The softmax function is one such function:

$$a_L=W_L{h}_{L-1}+b_L$$ $$\hat{y}=O(a_L{)}_j=\frac{e^{a_{Lj}}}{{\sum }_{i=1}^k{e}_{a_{L,i}}}$$

• Where $O(a_L{)}_j$ is the $j^{th}$ element of $\hat{y}$ and $a_{L,j}$ is the $j^{th}$ element of the vector $a_L$.

Since $y$ and $\hat{y}$ are probability distributions, we can use the cross-entropy function to compute the loss. Here are two excellent videos that explain what the concept of entropy is and why it is applicable in this context:

• Prof. Mithesh Khapra - Entropy, Information Content and Cross-Entropy
• Statquest - Entropy (for data science) Clearly Explained

The cross-entropy function is:

$$\mathcal{L}(\theta )=-\sum _{c=1}^k{y}_{c}log{\hat{y}}_c$$

In the true output vector, one element is 1 and the rest are zero, meaning that for each $c$ $y_c$ is either 1 or 0, this means that the loss function can be simplified as:

$$\mathcal{L}(\theta )=-log{\hat{y}}_l$$

• Where ${\hat{y}}_l$ represents that probability assigned to the true class label. For example, if we have an image of an Apple, $y_c$ would be 1 for it and 0 for all other fruits and the loss function would only the probability of an Apple into consideration.

Minimizing the above is the same as maximizing the negative of it. So, the loss function can be rewritten as:

$$\underset{\theta }{\max }-\mathcal{L}(\theta )=log({\hat{y}}_l)$$

• This quantity is known as the log-likelihood of the data.

So far, we’ve seen functions with two kinds of outputs - real values and probabilities. The type of output and loss function used in both contexts are given in the table below:

	Real Values	Probabilities
Output Function	Linear	Softmax
Loss Function	Squared Error	Cross-Entropy