Computing Gradient of Loss Function With Respect to Hidden Layers

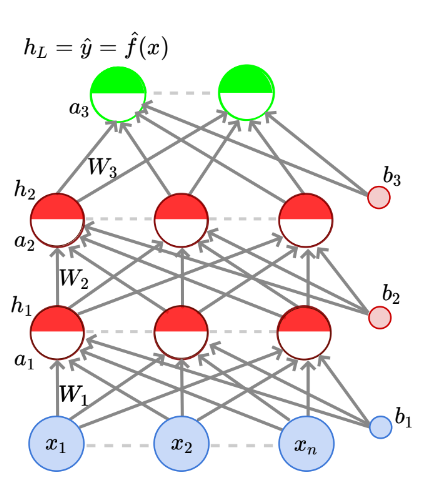
Now that we’ve computed the gradient of the loss function with respect to the output layer, we now move on to the hidden layer. Since there are several hidden layers, we would obviously like to derive a formula that would work for all hidden layers.

Let’s say we’d like to compute the gradient of the loss function with respect to one neuron in the $i^{th}$ layer in the network, which isn’t the input or output layers.

What we’d like to compute is:

$$\frac{\partial \mathcal{L}(\theta )}{\partial h_{ij}}$$

Generally, the derivative of a function $p(z)$, which can be written as a function of some intermediate function $q(z)$ is:

$$\frac{\partial p(x)}{\partial z}=\sum _m\frac{\partial p(z)}{\partial q_m}\frac{\partial q_m}{\partial z}$$

• Where $m$ represents each computation of the intermediate function.

In our case, the hidden layers determine the output of the layers above them, which in turn determine the loss function. So, the hidden layers would be $z$, the layers above them are generalised as $q(z)$ and the loss function is $p(z)$. Applying the above logic to this context:

$$\frac{\partial \mathcal{L}(\theta )}{\partial h_{ij}}=\sum _{m=1}^k\frac{\partial \mathcal{L}(\theta )}{\partial a_{i+1,m}}\frac{\partial a_{i+1,m}}{\partial h_{ij}}$$ $$=\sum _{m=1}^k\frac{\partial \mathcal{L}(\theta )}{\partial a_{i+1,m}}{W}_{i+1,m,j}$$

• $i$ refers to the layer being looked at, $m$ refers to each neuron in the layer and $j$ is the neuron in the $i^{th}$ layer whose gradient we’re trying to compute.

Now consider two vectors:

$${\nabla }_{a_i+1}\mathcal{L}(\theta )=\left[\begin{array}{c}\frac{\partial \mathcal{L}(\theta )}{\partial a_{i+1,1}}\\ ...\\ \frac{\partial \mathcal{L}(\theta )}{\partial a_{i+1,k}}\end{array}\right]$$ $$W_{i+1,\ast ,j}=\left[\begin{array}{c}{W}_{i+1,1,j}\\ ...\\ W_{i+1,k,j}\end{array}\right]$$

• The * means that we take all rows in the $j^{th}$ column of $W_{i+1}$.

Taking the dot product of the two vectors, we get:

$$(W_{i+1,\ast ,j}{)}^T{\nabla }_{a_{i+1}}\mathcal{L}(\theta )=\sum _{m=1}^k\frac{\partial \mathcal{L}(\theta )}{\partial a_{i+1,m}}{W}_{i+1,m,j}$$

This is equal to the derivative of the loss function with respect to one neuron in the hidden layer. Hence:

$$\frac{\partial \mathcal{L}(\theta )}{\partial h_{ij}}=(W_{i+1,\ast ,j}{)}^T{\nabla }_{a_{i+1}}\mathcal{L}(\theta )$$

We can apply this to the entire layer the neuron is in:

$${\nabla }_{h_i}\mathcal{L}(\theta )=\left[\begin{array}{c}\frac{\partial \mathcal{L}(\theta )}{\partial h_{i1}}\\ ...\\ \frac{\partial \mathcal{L}(\theta )}{\partial h_{in}}\end{array}\right]=\left[\begin{array}{c}(W_{i+1,\ast ,1}{)}^T{\nabla }_{a_{i+1}}\mathcal{L}(\theta )\\ (W_{i+1,\ast ,n}{)}^T{\nabla }_{a_{i+1}}\mathcal{L}(\theta )\end{array}\right]$$

• Where $n$ is the number of layers in the network.

The problem here is that except for the output layer $(i=L)$, we don’t know how to calculate ${\nabla }_{a_i}\mathcal{L}(\theta )$. We need to be able to compute the gradient with respect to the next hidden layer (i.e., ${\nabla }_{a_{i+1}}\mathcal{L}(\theta )$) in order to compute the same for this one. As always, let’s start off by computing the gradient for a single neuron:

$$\frac{\partial \mathcal{L}(\theta )}{\partial a_{ij}}=\frac{\partial \mathcal{L}(\theta )}{\partial h_{ij}}\frac{\partial h_{ij}}{\partial a_{ij}}$$ $$=\frac{\partial \mathcal{L}(\theta )}{\partial h_{ij}}{g}^{\prime }(a_{ij})[\because h_{ij}=g(a_{ij})]$$

Applying this to the entire vector, we have:

$${\nabla }_{a_i}\mathcal{L}(\theta )=\left[\begin{array}{c}\frac{\partial \mathcal{L}(\theta )}{\partial h_{i1}}{g}^{\prime }(a_{i1})\\ ...\\ \frac{\partial \mathcal{L}(\theta )}{\partial h_{in}}{g}^{\prime }(a_{in})\end{array}\right]$$

This is an element-wise multiplication of the two vectors. Therefore:

$${\nabla }_{a_i}\mathcal{L}(\theta )={\nabla }_{h_i}\mathcal{L}(\theta )\odot [...,g^{\prime }(a_{ik}),...]$$

Now that we can calculate the gradient with respect to the layers above a particular hidden layer, we can calculate it for the hidden layer as well. Note that this doesn’t create circular dependency. To compute the gradient w.r.t $a_i$ we need $h_i$‘s gradient, but for $h_i$ we need $a_{i+1}$.