Computing Gradient of Loss Function With Respect to Parameters

After examining the roles that the output layer and hidden layers play in the performance of a model, we now turn to the parameters (i.e., weights and biases) and look at their culpability.

Let’s look at the weights first:

$$\frac{\partial \mathcal{L}(\theta )}{\partial W_{kij}}=\frac{\partial \mathcal{L}(\theta )}{\partial a_{ki}}\frac{\partial a_{ki}}{\partial W_{kij}}$$

In the RHS, we need to compute 2 partial derivatives. We know the result of the first one from the previous section. As for the second part, remember that $a_K=b_k+W_k\ast h_{k-1}$. If we differentiate this with respect to the weight, we’re left with just the activation output from the previous layer.

$$\frac{\partial \mathcal{L}(\theta )}{\partial W_{kij}}=\frac{\partial \mathcal{L}(\theta )}{\partial a_{ki}}{h}_{k-1},j$$

$W_k$ i.e., the weights for a particular layer is a matrix and not a vector. This matrix would look like:

$${\nabla }_{W_k}\mathcal{L}(\theta )=\left[\begin{array}{ccc}\frac{\partial \mathcal{L}(\theta )}{\partial W_{k11}}& ...& \frac{\partial \mathcal{L}(\theta )}{\partial W_{k1n}}\\ ...& ...& ...\\ ...& ...& \frac{\partial \mathcal{L}(\theta )}{\partial W_{knn}}\end{array}\right]$$

Let’s assume that $W_k\in R^{3\times 3}$. In that case, the weight matrix would be (shamelessly taking a screenshot since I’m too lazy to type it out on my own):

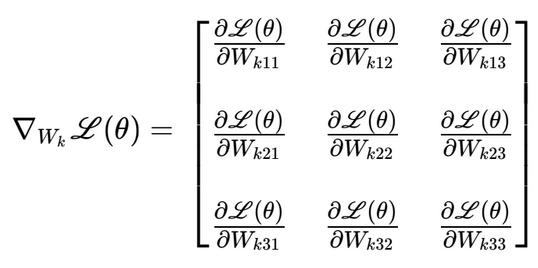
Applying the formula derived above to this matrix, we get:

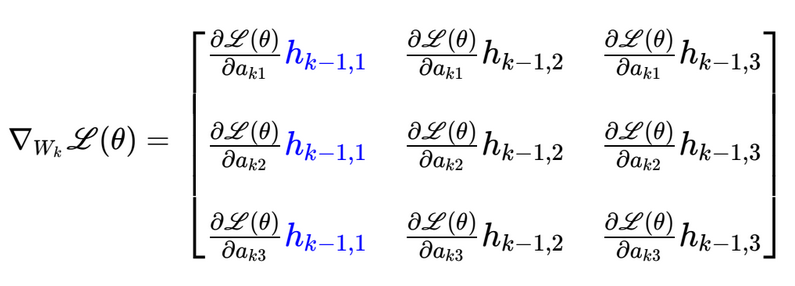
This matrix is just the outer product of the gradient of the loss function with respect to $a_k$ and the activation output of the $k-1^{th}$ layer:

$${\nabla }_{w_k}\mathcal{L}(\theta )={\nabla }_{a_k}\mathcal{L}(\theta )\ast h_{k-1}^T$$

Looking at the bias, remember once again that $a_K=b_k+W_k\ast h_{k-1},j$. This means that if we differentiate the loss function with respect to the bias, we get:

$$\frac{\partial \mathcal{L}(\theta )}{\partial b_{kij}}=\frac{\partial \mathcal{L}(\theta )}{\partial a_{ki}}\frac{\partial a_{ki}}{\partial b_{kij}}$$ $$=\frac{\partial \mathcal{L}(\theta )}{\partial a_{ki}}$$

Hence, the gradient vector would be:

$${\nabla }_{b_k}\mathcal{L}(\theta )=\left[\begin{array}{c}\frac{\partial \mathcal{L}(\theta )}{\partial a_{k1}}\\ ...\\ \frac{\partial \mathcal{L}(\theta )}{\partial a_{kn}}\end{array}\right]={\nabla }_{a_k}\mathcal{L}(\theta )$$