Momentum Based Gradient Descent

One problem with the Gradient Descent algorithm is that in flat error surfaces, the weight vector updates at a very slow pace since the gradient is small in flat surfaces. This delays the time until which the algorithm converges. Momentum based gradient descent offers a solution to this.

Let’s say we’re trying to go somewhere from our home and we’re not sure of the route. There’s no signal either so Google Maps isn’t working. So we ask someone on the road for direction and that person tells us to go left. Naturally, we would go rather slowly since we’re not sure yet if that person actually knows what they’re talking about. After going in the left direction, we ask another person and they tell us to continue on the same path. Now, we would pick up the pace a bit, since two people giving the same directions makes us more confidence that that is indeed the correct way to go. This is similar to how a ball being rolled down a slope would become faster as it gains momentum.

Remember that according to the weight-update rule of the Gradient Descent algorithm, the weight vector is updated based on the gradient of the loss function with respect to the weights for only that iterations, without taking the previous iterations’ gradients into account. Momentum based Gradient Descent, seeks to rectify this, by taking the entire history of updates to the weight into account while calculating the gradient for a particular iteration.

Let’s say we have a vector $u$ which contains all the updates to the weights, and a scaler $\beta$ which acts as a weightage for $u$ in an iteration. In an iteration $t$:

$$u_t=\beta u_{t-1}+\nabla w_t$$

This takes the previous iteration’s $u$ and adds the current iteration’s gradient to it. We then updates the weights, the taking all the previous iterations into account.

$$w_{t+1}=w_t-\eta u_t$$

$u$ is initialised to 0, which means that for the iteration, $u_0=\nabla w_0$. $w_0$ is initialised randomly and $0\le \beta <1$. Let’s write this formula for the first few iterations to get a clearer picture:

$$u_0=\nabla w_0$$ $$u_1=\beta (\nabla w_0)+\nabla w_1$$ $$u_2=\beta (\beta \nabla w_0+\nabla w_1)+\nabla w_2={\beta }^2\nabla w_0+\beta \nabla w_1+\nabla w_2$$

Generalising this, we get:

$$u_t=\sum _{\mathcal{T}=0}^t{\beta }^{t-\mathcal{T}}\nabla w_{\mathcal{T}}$$

This is basically the exponentially weighted average of the current and past gradients.

Given the algorithm takes the ‘momentum’ of the previous updates into account, it moves faster towards convergence than vanilla gradient descent. However, this increased speed comes with its share of issues. Going back to our example of getting somewhere from our home - if we’re fully confident that we’re going the right way, we might speed up a bit too much and overshoot our destination, forcing us to take a U-turn. Let’s look at the following graph and its corresponding contour plot:

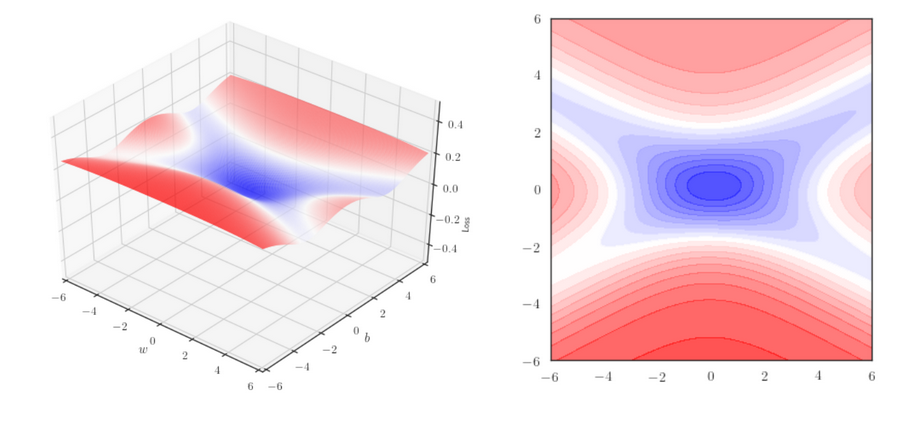
Notice that the slope is rather steep at the centre but is quite flat on all four sides as we move further away from the centre. Momentum-based Gradient Descent would allow us to reach the point of converge quickly but we can easily overshoot the required destination and overshoot again when try to get back on the right path, oscillating back and forth across the convergence point, as this demonstration shows us. Vanilla GD reaches the destination slower but does so cleanly while MGD gets their quicker but keeps overshooting as it tried to reach the destination.