Scheduling Learning Rate - Optimising Hyperparameters

The discussion around the variants of Gradient Descent took place because of the fact that the algorithm would move rather slowly in the flatter areas of the error surface. Momentum-based GD, Nesterov Accelerated GD and Stochastic GD are all possible solutions which address this problem.

One another way to speed up the process of navigating gentle slopes is to set a high learning rate, which would blow up the gradient. This demo shows GD in action where the learning rate is set to 10, a lot higher than it usually is. The problem here is that the model moves fast even in the steeper regions, where the gradient would be high enough as it is. Therefore, we’d like to have a way of adjusting the learning based on the gradient.

Here are some pointers to set the learning rate:

• Tune the initial learning rate on a log-scale: 0.0001, 0.001, 0.01, 0.1…
• Run a few epochs with each of these and check which ones works best.
• Run a finer search around the best value and check its neighbours.

Here are some pointers to anneal the learning rate:

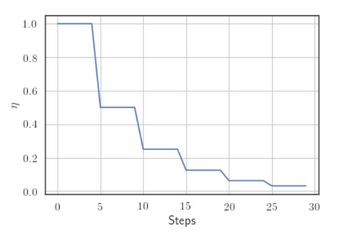
Step Decay: Halve the learning rate after every 5 epochs or halve it if the validation error is more than what it was after the previous epoch.

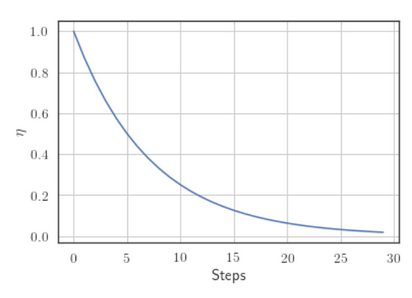
Exponential Decay: $n=n_0^{-kt}$ where $n_0$ and $k$ are hyperparameters and $t$ is the iteration number.

1/t Decay: $n=\frac{n_0}{1+kt}$ where $n_0$ and $k$ are hyperparameters and $t$ is the step number.

To set the momentum hyperparameter $\beta$, one could use the following formula:

$${\beta }_t=min(1-2^{-1-lo{g}_2(\frac{t}{250}+1)},{\beta }_{max})$$

• Where ${\beta }_{max}$ is chosen from $\{0.999,0.995,0.99,0.9,0\}$.

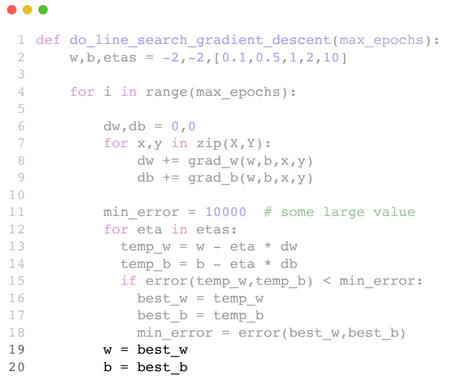
One other important way of optimizing the learning rate is to simply $w$ with different learning rates and retain the one which returns the least loss. At each epoch, we try out different learning rates and pick the one that works best. The catch here is that this increases the number of computations by a lot.