Root Mean Square Propagation - RMSProp

The fact that the accumulated gradient from all previous iterations were taken into account meant that the effective learning rate $\frac{\eta }{\sqrt{v_t+ϵ}}$ for dense features in a dataset would decay rapidly, since the gradients would be updated regularly pushing $v_t$ up at a high clip. A low learning rate would prevent updates to the gradient from taking place in future iterations.

RMSProp addresses this by decaying the denominator of the learning rate formula, thereby checking the decay of the entire learning rate. The update rule for RMSProp is:

$$v_t=\beta v_{t-1}+(1-\beta )\nabla w_t^2$$ $$w_{t+1}=w_t-\frac{\eta }{\sqrt{v_t+ϵ}}\nabla w_t$$

• Similar logic for the bias as well.

The introduction of $\beta$ slows down the growth of $v_t$, which checks the decay of the effective learning rate. Let’s write down the evolution of the gradient’s history over a few iterations.

$$v_t=\beta v_{t-1}+(1-\beta )\nabla w_t^2$$ $$\beta =0.9$$ $$v_0=0.1\nabla b_0^2$$ $$v_1=0.1\nabla b_1^2+0.09\nabla b_0^2$$ $$v_2=0.1\nabla b_2^2+0.08\nabla b_0^2+0.09\nabla b_1^2$$ $$v_t=(1-\beta )\sum _{\mathcal{T}=0}^t{\beta }^{t-\mathcal{T}}\nabla b_{\mathcal{T}}^2$$

Compared to AdaGrad, the learning rate decays slower in RMSProp.

From this demo comparing the two, notice how RMSProp converges faster than AdaGrad since its learning rate doesn’t decay as fast. However, it did oscillate a fair bit. This means that it’s possible for the learning rate to remain constant in such a way that it oscillates around the minima and never touches it.

In AdaGrad, the accumulation of gradients $v_t=v_{t-1}+(\nabla w_t{)}^2$ never decreases even if the gradients themselves are low, which means that the learning monotonically decreases.

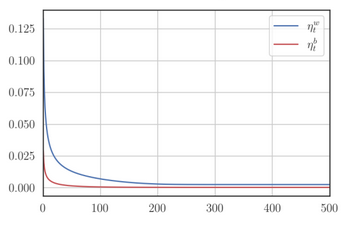
In RMSProp, however, due to the variability of the denominator of the learning rate introduced by $\beta$, the learning rate might increase, decrease or remain constant. A constant learning rate, as mentioned before, could make it oscillate endlessly around the minimum.

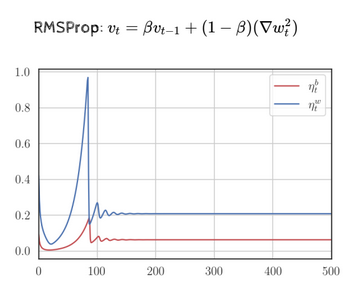
• Also notice that the learning rate actually increases at the beginning since $v_t$ could reduce from one iteration to another due to $\beta$.

These oscillations are caused by the initial learning rate. Here are some demos which show the evolution of the learning rate based on the initial rate set:

• ${\eta }_0=0.6⟹\frac{0.6}{\sqrt{v_t+ϵ}}$ : https://s3.amazonaws.com/media-p.slid.es/videos/1839032/hC06LNa3/constlr_rms_adagrad__1_.mp4
• ${\eta }_0=0.1⟹\frac{0.1}{\sqrt{v_t+ϵ}}$ : https://s3.amazonaws.com/media-p.slid.es/videos/1839032/ouyD0AuU/constlr_low_rms_adagrad.mp4

Which among the two is better?

In the the steeper areas where the gradient is high, we’d like the lower initial learning rate (i.e., $0.6$) while in the flatter regions with low gradient, we would prefer a higher learning rate. However, when we set an initial learning rate, we have to stick it for the entirety of the process and can’t pick different initial learning rates based on the gradient/slope in ADAGRAD and RMSProp, despite the fact that the former, in its own right, does a lot better than ADAGrad, which is displayed in this that compares all the GD-based algorithms we’ve seen so far.