Adaptive Delta - AdaDelta

Both ADAGRAD and RMSProp are both sensitive to the initial learning rate and could possibly never converge if the learning rate chosen initially is not suitable. ADADelta avoids setting an initial learning rate and instead takes the difference in gradients between iterations to update the weights. The update rule for this algorithm is:

$$v_t=\beta v_{t-1}+(1-\beta )(\nabla w_t{)}^2$$ $$\Delta w_t=-\frac{\sqrt{u_{t-1}+ϵ}}{\sqrt{v_t+ϵ}}\nabla w_t$$ $$u_t=\beta u_{t-1}+(1-\beta )(\Delta w_t{)}^2$$ $$w_{t+1}=w_t+\Delta w⟹w_{t+1}=w_t-\frac{\sqrt{u_{t-1}+ϵ}}{\sqrt{v_t+ϵ}}\nabla w_t$$

• The effective learning rate here is $\frac{\sqrt{u_{t-1}+ϵ}}{\sqrt{v_t+ϵ}}$ instead of $\frac{\eta }{\sqrt{v_t+ϵ}}$, which means that $\eta$ gets replaced by $\sqrt{u_{t-1}+ϵ}$ .

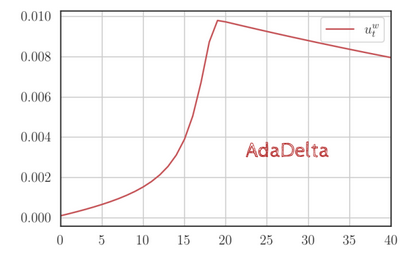
We can see that $u_t$ is a function of $\Delta w$, which in turn is a function of past updates to the gradient, as opposed to $\eta$ which is a constant. This means that the numerator of the effective learning rate isn’t constant and can change depending on the gradient/slope.

Also notice that at a particular iteration $t$ the numerator of the learning rate takes the accumulated history of gradients till the previous time step, which is why we take $u_{t-1}$. This means that $u$ is one iteration behind $v$. So how can this help in adapting the learning rate to the slope/gradient of the region we are currently in? Both $v_t$ and $u_t$ increase after each iteration, but the magnitude of $u_t$ is less than that of $v_t$ as it takes only a fraction of the squared gradient, since it’s moderated by $\frac{\sqrt{u_{t-1}+ϵ}}{\sqrt{v_t+ϵ}}$.

In steep regions, where the gradient is high, $v_t$ would zoom ahead, but $u_t$ isn’t too far back since it’s only one iteration behind, ensuring that the effective learning wouldn’t decay as aggressively, even though $v_t$ increases fast.

Now, if we move to a flatter region, $v_t$ will reduce due to the momentum factor $\beta$. However, since $u$ is behind $v$, it would not have decreased so much, and the ratio of the numerator to the denominator would start to increase. If the gradient remains low for enough time, the learning rate would increase.

Thus, ADADELTA allows the numerator of the effective learning rate, which is kept constant in ADAGRAD and RMSProp, to vary depending on the previous gradients. The learning rate, therefore, decays slower:

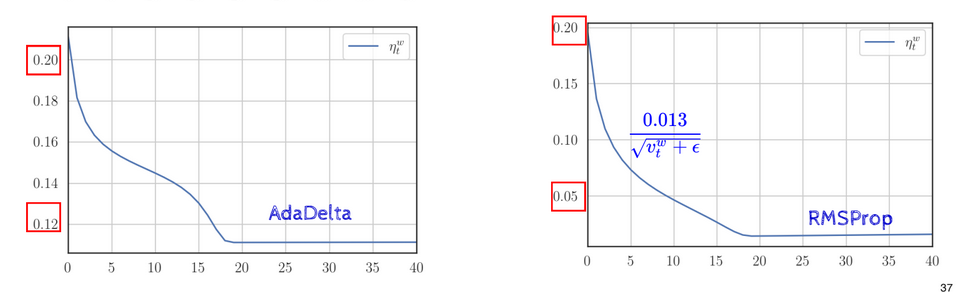
This is because of the fact that $u_t$ changes in proportion to $v_t$, keeping its influence in check.

This compares the two, with $n_0=0.013$ for RMSProp and $w_0=-4$ and $b_0=-4$ for ADADelta. ADADelta converges faster as its learning rate doesn’t decay as quickly.