Adaptive Moments Algorithm - ADAM

The next Gradient Descent-based algorithm we look at is Adam, which does everything RMSProp and Adadelta do to minimise the decay of the learning rate, and uses a cumulative history of the gradients. The update rule for Adam is:

$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)\nabla w$$ $${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$$ $$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)(\nabla w{)}^2$$ $${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$$ $$w_{t+1}=w_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$$

• Typically, ${\beta }_1=0.9$ and ${\beta }_2=0.999$

In the previous algorithms, the effective learning rate was multiplied by the gradient of the current iteration to update the gradient. This time, we multiply it by the cumulative history of gradients i.e $m_t$.

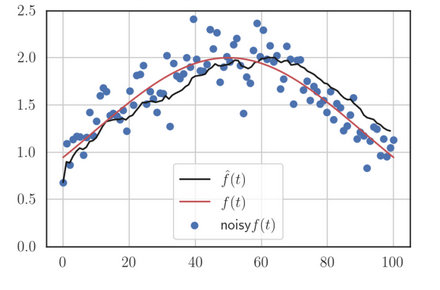
Further, ${\hat{m}}_t$ and ${\hat{v}}_t$ are responsible for what is called bias correction, which is why the final gradient update is done with these bias-corrected values instead of their original (biased) computations. Remember that the $\beta$ factor was introduced initially to create a moving average of the past and current gradients. $m_0$ and $v_0$ are usually 0, which means that if we did not bias-correct, the computations of $m_t$ and $v_t$ in future iterations, at least at the beginning, would be biased towards 0, which shouldn’t happen since there is no sanctity to the fact that they were initialised to 0. The bias correction eliminates this bias to 0. Also, without bias correction, the learning rate would be too large initially, which could lead to the minimum being overshot, as shown in this.

Suppose we perform stochastic/mini-batch Gradient Descent on a dataset and the current batch doesn’t represent the data well i.e is “noisy”. The gradient computed without bias correction, the gradients would be heavily biased towards zero:

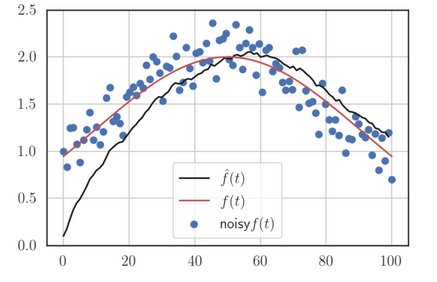
But if we apply bias-correction, the estimations would be better: