MaxProp and AdaMax

Recall that the update rule for RMSProp is:

$$v_t=\beta v_{t-1}+(1-\beta )\nabla (w_t{)}^2$$ $$w_{t+1}=w_t-\frac{\eta }{\sqrt{v_t+ϵ}}\nabla w_t$$

$v_t$ is essentially the weighted average of the squares of all the gradients to date. If we remove the weights i.e $\beta$, it is the same as calculating the $L^2$ norm. Instead of taking $L_2$ norm, we can take $L^{\infty }$ norm, where each current gradient would taken to the power $\infty$. The $L^{\infty }$ norm of any vector works out to its maximum element. In the calculation of $v_t$, we sum up the current gradient and past gradient. If we apply $L^{\infty }$ norm (also known as $max()$ norm) here, $v_t$ would be the maximum of the current gradient and all the past gradients. The update rule for MaxProp therefore is:

$$v_t=max(\beta v_{t-1},|\nabla w_t|)$$ $$w_{t+1}=w_t-\frac{\eta }{v_t+ϵ}{\hat{m}}_t$$

• Since this a modification of RMSProp, we use a constant initial learning rate.

Unlike Adam, we don’t use bias-correction in MaxProp. Suppose $v_0=0$ and $\nabla w_1=0.5$, $v_t=max(0,0.5)=0.5$, which means that is not biased towards zero even though it’s initialised to the same.

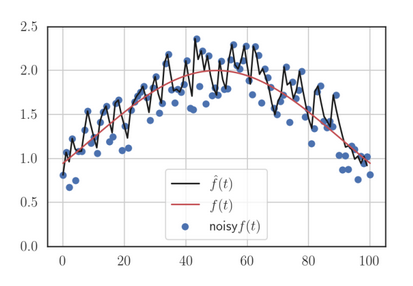
Moving on, one benefit of using the max norm instead L2 is that it keeps the learning constant when the gradient doesn’t change. This is especially relevant for sparse features. If we had used the L2 norm (RMSProp) instead, the learning rate would gradually increase (even with bias-correction), even though $\nabla w_t=0$.

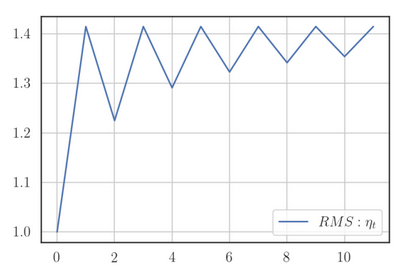
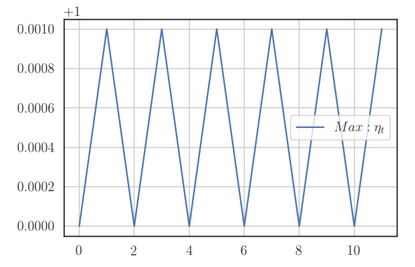
While the MaxProp algorithm modified RMSProp by taking the max norm instead of the L2 norm, we can modify the Adam algorithm in the same manner. This algorithm is called AdaMax and its update rule is:

$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)\nabla w_t$$ $${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$$ $$v_t=max({\beta }_2{v}_{t-1},|\nabla w_t|)$$ $$w_{t+1}=w_t-\frac{\eta }{v_t+ϵ}{\hat{m}}_t$$

• Notice that there is no bias correction for $v_t$ as it’s not susceptible to initial bias towards zero.