Gradient Descent - Updating Weights

Using the Taylor Series, we established that changes made to the weights $w$ and bias $b$ must be in the direction opposite to that of the gradient vector. The gradient vector is the derivative of the loss function with respect to the weights and bias.

After iteration $t$, the algorithm to update the weight at the $t+1^{th}$ iteration should be:

$$w_{t+1}=w_t-\eta \nabla w_t$$ $$b_{t+1}=b_t-\eta \nabla b_t$$

Where:

$$\nabla w_t=\frac{\partial \mathcal{L}(w,b)}{\partial w}$$ $$\nabla b_t=\frac{\partial \mathcal{L}(w,b)}{\partial b}$$

• Both derivatives are calculated at $w=w_t$ and $b=b_t$.

The pseudocode for this algorithm is:

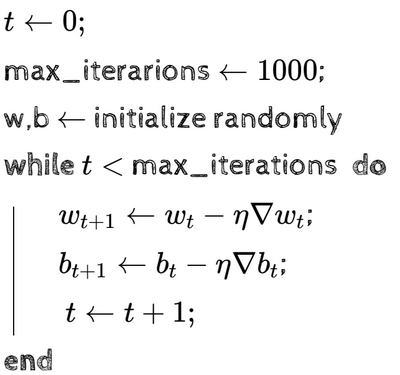
What is the formula to compute the gradient for the sigmoid function, which has been the focus till now? Remember that $f(x)=\frac{1}{1+e^{-(wx+b)}}$. Assuming there’s only one input point, the loss function is:

$$\mathcal{L}(w,b)=\frac{1}{2}(f(x)-y{)}^2$$

The derivative can therefore be calculated as:

$${\nabla }_w=\frac{\partial }{\partial w}[\frac{1}{2}(f(x)-y{)}^2]$$ $$=\frac{1}{2}[2\ast (f(x)-y)\ast \frac{\partial }{\partial w}(f(x)-y)]$$ $$=(f(x)-y)\ast \frac{\partial }{\partial w}(\frac{1}{1+e^{-(wx+b)}})$$

Recall from the good ol’ days that $\frac{d}{dx}(\frac{1}{x})=\frac{1}{x^2}\ast \frac{d}{dx}x$. Using the chain rule, upon computing the derivative of the sigmoid function, we get:

$${\nabla }_w=(f(x)-y)\ast f(x)\ast (1-f(x))\ast x$$

Similarly:

$${\nabla }_b=(f(x)-y)\ast f(x)\ast (1-f(x))$$

For two or more points:

$$\sum _{i=1}^n{\nabla }_w=(f(x)-y)\ast f(x)\ast (1-f(x))\ast x$$ $$\sum _{i=1}^n{\nabla }_b=(f(x)-y)\ast f(x)\ast (1-f(x))$$

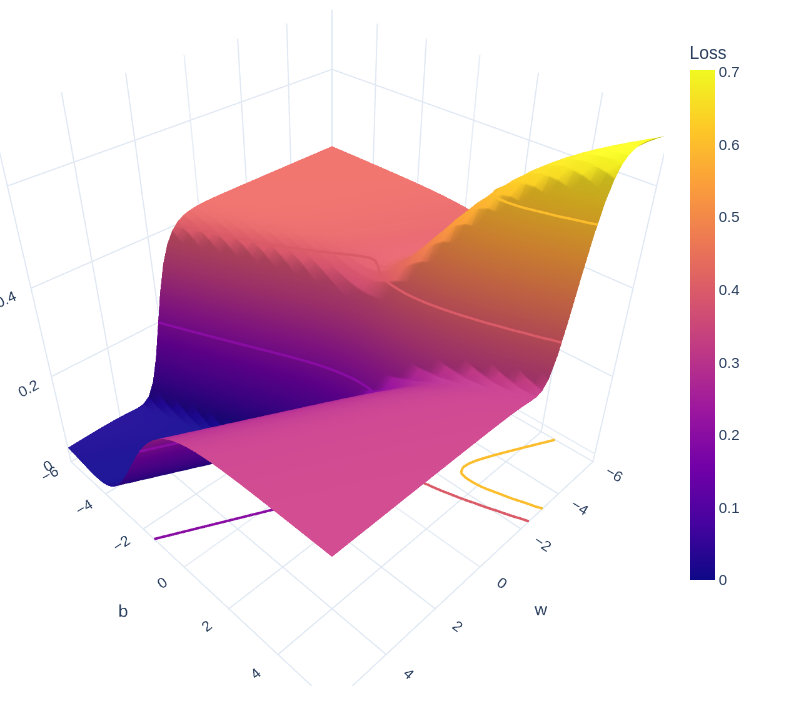
These 2 derivates can be plugged into the update formula to get the new weight vector. The following 3D plot shows the loss gradually decreasing as the weights and bias change:

Python code for the Gradient Descent Model from start to finish:

import numpy as np
 
# Using sigmoid function
def output(x, w, b):
	return 1 / (1 + np.exp(-(w * x + b)))
 
def gradient_weight(x, w, b, y):
	fx = output(x, w, b)
	return (fx - y) * fx * (1 - fx) * x
 
def gradient_bias(w, x, b, y):
	fx = output(x, w, b)
	return (fx - y) * fx * (1 - fx)
 
def grad_desc(X, Y, w, b, eta, max_epochs):
	weights = []
	biases = []
	for i in range(max_epochs):
		dw = 0
		db = 0
 
		for (x, y) in zip(X, Y):
			dw = gradient_weight(w, x, b, y)
			db = gradient_bias(w, x, b, y)
			w -= eta * dw
			
		w -= eta * dw
		b -= eta * db
 
	return (w, b)
 
def mean_squared_error(X, Y, w, b):
	error = 0
	for x, y in zip(X, Y):
		fx = output(x, w, b)
		error += (y - fx) ** 2
	return (error / len(X))