Adaptive Gradient Algorithm - AdaGrad

As described in the previous section, we need an algorithm that can vary the learning rate for different parameters based on how sparse they are. The gradient of those features that are more sparse get updated rarely since the features themselves will be 0 often. Adagrad decays the learning rate for features in proportion to how frequently they get updated. Hence, dense features that are updated frequently have their learning rates decay rapidly while sparse features’ learning rates decay slower.

Similar to Momentum-based Gradient Descent, Adagrad takes the history of gradients for a feature into account. The update rule for Adagrad is:

$$v_t=v_{t-1}+(\nabla w_t{)}^2$$ $$w_{t+1}=w_t-\frac{\eta }{\sqrt{v_t+ϵ}}$$

• The hyperparameter $ϵ$ exists to avoid division by 0.
• The same set of equations will apply to the bias as well.

Since the gradient for sparse features will often be 0, the effective learning rate $\frac{\eta }{\sqrt{v_t+ϵ}}$ will be rather high while for denser features, it will be low, since the high total gradient will push the denominator up.

However, even for sparse features, $v_t$ will increase, even if slower than for dense features. The rate of decay will be slower for them, allowing updates to the gradient to be bigger thanks to the jacked up learning rate.

The following plot plots the gradients ($\nabla w$), sum of gradient squares ($v_t$) and effective learning rate (${\eta }_t$) for sparse features.

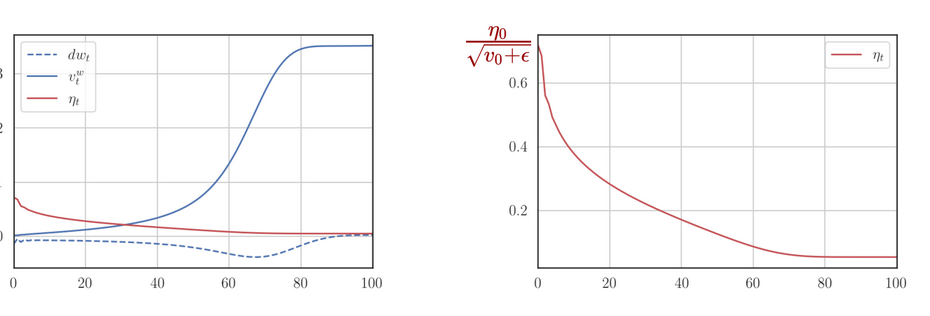
• $v_t$ grows gradually since updates are, while the effective learning rate $\frac{\eta }{\sqrt{v_t+ϵ}}$ decays slowly, allowing updates to be big, even if rare.

Similarly, let’s look at the same plots for dense features:

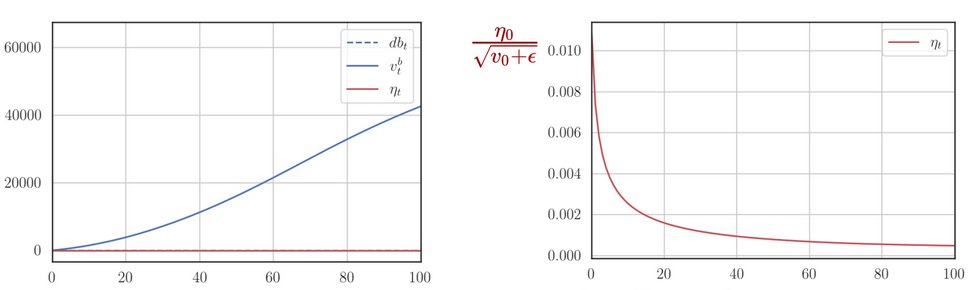
• $v_t$ grows rapidly since updates are frequent, while the effective learning rate decays rapidly.

This demo compares the performance of Adagrad, MGD, NAG and SGD. Notice that near the minimum, Adagrad slows down, due to the learning having decayed heavily, since both sparse and dense features would’ve accumulated some significant history by then.

By using variable learning rates, Adagrad ensures that sparse features get large updates, allowing their importance to be maintained. The catch here is that the decay in the effective learning rate of dense features could be massive, to the extent that updates to the gradient stop happening.